


Il lotto economico di acquisto indica la quantità ottimale che dovrebbe essere ordinata in ogni approvvigionamento di merci in quanto rende minima la combinazione tra i costi di ordinazione e i costi di stoccaggio. In questo tutorial proponiamo un semplice modello realizzato su di un foglio di calcolo che utilizzeremo per illustrare tale teoria dal punto di vita matematico ed economico. I costi di magazzino possono essere suddivisi in due tipologie: i costi di ordinazione ed i costi di stoccaggio.
=> Scarica l’esempio
I costi di ordinazione
I costi di ordinazione sono dati dall’insieme di costi che consentono di gestire una ordinazione di merci quali, ad esempio, i costi amministrativi per la ricerca dei fornitori, per l’emissione e la contabilizzazione degli ordini di acquisto, per il controllo di qualità delle merci. Il costo totale annuo di ordinazione è espresso dalla formula:
Co = N/Q * Cf
N = quantità da ordinare nel corso dell’anno
Q = quantità acquistata ogni volta (lotto di acquisto)
N/Q = numero degli ordini di acquisto da effettuare nel corso dell’anno
Cf = costo (fisso) di ciascuna ordinazione
Per esempio, supponiamo di dover ordinare 1000 unità di un certo prodotto nel corso dell’anno e di acquistare mediamente 200 unità per ogni ordinazione; supponiamo, inoltre, che i costi di ordinazione per ciascun ordine relativo al prodotto siano stimati in 160 €. Ci interessa capire l’ammontare dei costi annuali di ordinazione. Riportando i dati nel modello (rispettivamente nelle celle B4, B5 e B6) si ottiene un costo complessivo di ordinazione pari a 800 € (160 € per 5 ordinazioni).

=> Determinazione del “Costo Industriale”
Il numero degli ordini da effettuare in un anno (B6) si ottiene dividendo le quantità da ordinare complessivamente in un anno (B4) per le quantità acquistate con ogni ordine (B5); il totale dei costi di ordinazione (B8) si ottiene, invece, moltiplicando i costi di ordinazione unitari (B7) per il numero di ordini evasi in un anno (B6).
Risulta evidente che se si aumenta la quantità da acquistare ogni volta (B5) si riduce il numero delle ordinazioni (B6) in un anno e si ottiene un costo complessivo di ordinazione più basso (dato per ipotesi la costanza dei Costi fissi per ordinazione, inseriti nella cella B7). Se, ad esempio, acquistassimo 250 prodotti ogni volta avremmo bisogno di fare solo 4 ordinazioni in un anno (250*4=1000) e pertanto avremmo un costo totale di ordinazione pari a 640 € (160*4) anziché 800 €. Quindi risulta che il Costo totale di ordinazione tende a ridursi all’aumentare del quantitativo di merce acquistata per ogni ordinazione.
I costi di stoccaggio
I costi di stoccaggio sono rappresentati dai costi per la gestione delle magazzino (compreso i costi per il personale), dai costi assicurativi, da eventuali perdite per deterioramento o svalutazione per obsolescenza della merce e dagli oneri figurativi sul capitale impiegato per l’acquisizione delle scorte.
Il costo totale annuo di stoccaggio è espresso dalla formula:
Cs = Cu * P * Q/2
Dove
Cu = costo annuo di stoccaggio unitario
P = prezzo di acquisto unitario (o meglio il costo di acquisto della merce)
Q = quantità di prodotti acquistati ogni volta (lotto di acquisto)
Q/2 = quantità di prodotti mediamente presenti in magazzino
Continuando con l’esempio precedente, supponiamo che il costo medio di acquisto per ogni unità di prodotto sia pari a 450 €, che i costi unitari di giacenza (relativi ai costi del personale, delle assicurazioni, etc.) siano stimati in 8 € per unità di prodotto e che vengano calcolati degli oneri figurativi sul capitale investito nel magazzino ad un tasso del 5% annuo. A quanto ammonteranno i costi annuali di stoccaggio? Riportando i dati nel modello (rispettivamente nelle celle B11, B17 e B15) si ottiene un costo complessivo di stoccaggio pari a 3.050 €.

Analizziamo brevemente le formule inserite nella tabella.
=> Appalti e contabilità: rimanenze di opere pluriennali
Nella cella B12 è stato utilizzato un riferimento alla cella B5 (=B5) nella quale è stato inserito già il lotto di acquisto; le quantità di stock medie inserite in B13 è stata calcolata dividendo per due il valore della cella B12 (=B12/2); il costo della scorta media inserito nella cella B14 indica il capitale investito mediamente nel magazzino ed è stato calcolato moltiplicando il prezzo unitario di acquisto per la consistenza media di magazzino (=B11*B13); gli oneri figurativi indicano il costo per il capitale immobilizzato nel magazzino ed è stato calcolato moltiplicando la cella B14 per il tasso di interesse (B15); i costi totali annui di giacenza inseriti nella cella B18 sono stati calcolati moltiplicando i costi unitari (B17) per le quantità mediamente presenti in magazzino (B13); i costi totali annui di stoccaggio (cella B19) si ottengono sommando gli oneri figurativi con i costi complessivi di giacenza (=B16+B18); il costo unitario di stoccaggio (Cu) inserito nella cella B19 è stato calcolato dividendo i costi totali annui di stoccaggio per il costo della scorta media (=B19/B14), esso indica idealmente il costo di stoccaggio su una unità di capitale (nell’esempio, per ogni euro investito nel magazzino, 7 centesimi sono destinati ai costi di stoccaggio); infine, nella cella B21, per completezza espositiva, è stato calcolato nuovamente il totale costi di stoccaggio utilizzando la formula matematica illustrata in precedenza (=B20*B11*B13).
I costi di stoccaggio tendono ad essere più alti quando in magazzino esistono mediamente più prodotti: crescono i costi assicurativi, i costi del personale che deve essere impiegato nella gestione dei prodotti in magazzino, i costi degli oneri figurativi in quanto si investe mediamente maggiore capitale nel magazzino, etc. Poiché la consistenza di magazzino dipende dalle quantità acquistate con ogni ordinazione (maggiore è la quantità acquistata maggiore è la giacenza di quei prodotti in magazzino), possiamo affermare che il Costo totale di stoccaggio tende a crescere all’aumentare del quantitativo di merce acquistata per ogni ordinazione.
Il lotto economico di acquisto
Riassumendo, possiamo affermare che all’aumentare del lotto di ordinazione si assiste, da un lato, ad un aumento del costo totale di stoccaggio e, dall’altro, ad una riduzione del costo annuo di ordinazione (relazioni opposte si verificano se si tende a ridurre il lotto di ordinazione). La domanda alla quale dobbiamo dare una risposta è: «Quale è il lotto di acquisto che consente di avere minori costi di magazzino?». Matematicamente esso è dato dal valore in corrispondenza del quale si verifica l’uguaglianza tra i costi di ordinazione e i costi di stoccaggio.
=> E-commerce: la corretta gestione del magazzino
Il lotto economico di acquisto, pertanto, è dato dalla seguente relazione matematica:
Co = Cs
ovvero
N/Q * Cf = Cu * P * Q/2
che, dopo alcuni passaggi matematici (che evitiamo per semplicità di esposizione), può essere scritta nel seguente modo:
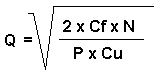
Riassumiamo le relazioni tra i costi da un punto di vista grafico utilizzando per l’asse Y le funzioni dei costi (di stoccaggio e di ordinazione) e per l’asse X le quantità da acquistare periodicamente (lotto di acquisto).
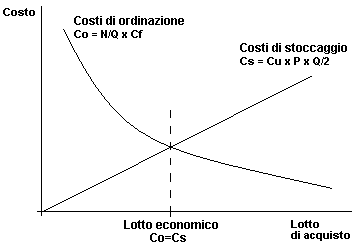
I Costi di ordinazione sono rappresentati da una iperbole (al crescere del lotto di acquisto si riducono) mentre i Costi di stoccaggio sono rappresentati da una retta (al crescere del lotto di acquisto aumentano). Il lotto economico di acquisto è dato dalle quantità in corrispondenza della intersezione delle due curve (punto in cui tali costi sono uguali fra di loro); detto in altri termini, le quantità del lotto economico consentono di avere il più basso costo totale di magazzino (da cui, appunto, si parla di economico). Utilizziamo ora i dati riportati negli esempi precedenti, per ricavare il lotto economico di acquisto, ovvero le quantità da acquistare mediamente per ridurre i costi complessivi di magazzino.
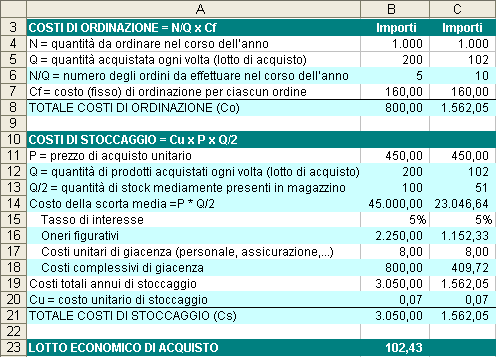
Il lotto economico di acquisto è stato calcolato nella cella B23 attraverso la formula:
=((2*B7*B4)/(B11*B20))^(1/2)
in cui abbiamo espresso la radice quadrata con la notazione esponenziale (la radice di un numero si ottiene elevando quest’ultimo a 1/2).
Dall’esempio, si evince che se si ordinano mediamente 102,43 prodotti (anziché 200) si ottiene un risparmio nella gestione del magazzino. Per verificare, dal punto di vista matematico, tale affermazione è sufficiente risolvere le due equazioni matematiche relative ai costi di stoccaggio e di ordinazione sostituendo la variabile iniziale Q (del valore di 200) con le quantità del lotto economico ottenute dall’ultima formula (102,43).
Dal punto di vista aziendalistico sarebbe opportuno conoscere le singole variazioni per avere un quadro di riferimento più dettagliato. Per farlo è sufficiente duplicare i dati (e le formule) della colonna B all’interno della colonna C e inserire nella cella C5 il riferimento (=B23) al lotto economico di acquisto (nel duplicare le celle occorre fare attenzione a quelle contenenti valori numerici in quanto questi ultimi vengono aumentati automaticamente di una unità!). Analizziamo brevemente i dati ottenuti nella colonna C. Con riferimento ai costi di ordinazione possiamo osservare come una riduzione delle quantità da ordinare ogni volta (da 200 a 102) comporta un aumento di tali costi che passano da 800 a 1.562; tale aumento è dovuto ai maggiori ordini che devono essere eseguiti durante l’anno per raggiungere le 1000 unità di prodotto (10 ordini anziché 5). Con riferimento ai costi di stoccaggio possiamo osservare, invece, che la riduzione delle quantità da ordinare, riduce il numero medio di prodotti in magazzino (che passano da 100 a 51) e ciò si ripercuote positivamente sia sui costi di giacenza che sugli oneri figurativi che vengono abbattuti di quasi ma metà del loro valore; nel complesso, i costi di stoccaggio passano da 3.050 € a 1.562 €. Complessivamente, l’incremento dei costi di ordinazione (+762) è compensato ampiamente dalla riduzione dei costi di stoccaggio (-1488) e ciò comporta un risparmio di risorse finanziare investite nel magazzino (+726).
=> Calcolo automatizzato dei contributi figurativi
Limiti di applicazione del lotto economico di acquisto
Prima di concludere questo tutorial soffermiamoci brevemente sui limiti del “lotto economico di acquisto”. Il risultato della soluzione matematica dipende principalmente dall’attendibilità di alcune variabili (quali, ad esempio, il valore dei costi fissi di ordinazione, dei costi unitari di giacenza, del tasso di interesse per determinare gli oneri figurativi) che, a loro volta, dipendono dal sistema di rilevazione utilizzato in azienda (un’azienda che affianca alla contabilità generale un sistema di contabilità industriale sarà in grado di avere dati maggiormente attendibili). Ma esistono altre condizioni che necessitano di essere soddisfatte: i prodotti devono essere caratterizzati da una domanda regolare senza sbalzi stagionali, la merce deve essere non facilmente deperibile in special modo se il lotto economico assume valori alti, i fornitori devono essere in grado di offrire i quantitativi richiesti, e questi sono solo alcuni esempi al riguardo. Infine esistono altri elementi “esterni” da considerare nella gestione degli approvvigionamenti: la possibilità di ottenere degli sconti su forniture consistenti, le oscillazioni dei prezzi delle materie prime, la facilità di reperire risorse finanziarie dal sistema bancario, etc. Possiamo pertanto concludere che la soluzione matematica può fornire un’utile indicazione sul quantitativo ottimale di acquisto ma la scelta definitiva in merito alle quantità da acquistare ogni volta deve essere assunta tenendo conto anche dei limiti del modello.









