


In tutte le aziende c’è la tendenza a effettuare previsioni sull’andamento di variabili (fatturato complessivo, vendite di un determinato prodotto, quote di mercato, solvibilità media della clientela, etc.). Una buona previsione dipende da numerosi fattori, in particolare dall’accuratezza dalla serie storica dei dati, dal tipo di stima (a breve, medio o lungo termine) e dal metodo matematico-statistico adoperato. Utilizzare, ad esempio, una serie storica lunga per previsioni di vendita di un certo prodotto (fatturato degli ultimi 10 o 20 anni) potrebbe essere poco significativo se si considera la dinamicità dei mercati, la concorrenza incalzante di altri operatori, il ciclo di vita del prodotto più breve.
=> Aggiungere una linea di tendenza ad un grafico Excel
Anche quando si utilizza una serie storica adeguata è necessario tenere in giusta considerazione alcune variabili che possono influire negativamente sulle previsioni: ad esempio, una vendita straordinaria dovrebbe essere esclusa dalla serie di dati, o la serie dovrebbe essere normalizzata escludendo valori che difficilmente si ripeteranno. Anche il tipo di previsione influenza notevolmente la sua accuratezza: una previsione delle vendite per i prossimi due/tre anni porta sicuramente a dati più accurati rispetto ad una previsione decennale (non è un caso che grosse aziende utilizzano anche dei budget semestrali).
I metodi di calcolo sono molteplici (lineare, esponenziale, logaritmico, …) e ognuno si utilizza per un determinato tipo di dati o previsione. In azienda si utilizzano solitamente previsioni basati sul sistema lineare, in quanto i valori storici raramente subiscono grosse variazioni in tempi brevi (se un’azienda ha venduto nell’anno cento prodotti, difficilmente il prossimo anno ne riuscirà a vendere mille). Il metodo previsionale di tipo lineare si basa sulla funzione TENDENZA, che esaminiamo in questo tutorial.
La funzione TENDENZA
La funzione TENDENZA, appartenente alla categoria Statistiche, ha la seguente sintassi: =TENDENZA(y_nota;x_nota;nuova_x;cost)
Per illustrare gli argomenti della funzione TENDENZA facciamo riferimento al procedimento matematico che è alla base del calcolo. La funzione disegna su di un grafico “immaginario” una serie di punti dati dalle coordinate y e x indicati nei primi due argomenti (pertanto, gli argomenti y_nota e x_nota devono fare riferimento ad uno stesso numero di valori o di celle), crea l’equazione della “retta di interpolazione lineare” attraverso il “metodo dei minimi quadrati” (la retta y=mx+q i cui punti sono equidistanti dai punti disegnati in precedenza) ed, infine, restituisce, utilizzando l’equazione della retta di interpolazione, il valore y corrispondente alla nuova variabile indipendente x indicata come terzo argomento della funzione (nuova_x).
L’ultimo argomento cost, che nella maggior parte dei calcoli di tipo aziendalistico viene omesso, è un valore logico che serve a specificare il valore che deve assumere la costante q della retta di interpolazione: se l’argomento è pari a 1 o a FALSO, la costante q viene considerata uguale a zero (q=0) e, pertanto, la retta di interpolazione (la cui equazione diventa y=mx) passa per l’origine degli assi; se è omesso, o pari a 0 o a VERO, la retta di interpolazione viene disegnata normalmente.
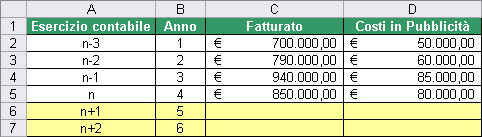
Facciamo qualche esempio pratico per comprendere il funzionamento di TENDENZA utilizzando i dati riportati sul foglio di calcolo rappresentato in figura (la tabella riporta il fatturato conseguito negli ultimi quattro anni nell’intervallo C2:C5 mentre, nell’intervallo D2:D5 la spesa pubblicitaria sostenuta nello stesso periodo).
=> L’andamento delle quotazioni azionarie su Excel
Esempio uno
Supponiamo di investire, nel prossimo anno, la somma di 90.000 euro in pubblicità e di voler conoscere, utilizzando una previsione di tipo lineare, quale sarà il valore del fatturato nell’esercizio contabile n+1. Nell’esempio riproposto, la variabile indipendente è data dai “Costi in Pubblicità”, mentre la variabile dipendente è data dal “Fatturato”: su di un ipotetico grafico, quindi, sull’asse x andrebbero indicati i costi in pubblicità mentre sull’asse y il fatturato.

Ne segue che, dopo aver inserito nella cella D6 il valore di 90.000, nella cella C6 utilizzeremo la funzione:
=TENDENZA(C2:C5;D2:D5;D6)
Pertanto, spendendo la somma di 90.000 euro in pubblicità si potrebbe ottenere, secondo la stima lineare, un fatturato di 944.580,15 (il risultato della funzione TENDENZA).
Esempio due
Supponiamo, sempre con riferimento ai dati riportati in tabella, di voler conoscere la spesa che dovremmo sostenere in pubblicità per conseguire, sempre nel prossimo anno, un fatturato di un milione di euro. In questo secondo esempio, la variabile indipendente è data dal “Fatturato” mentre la variabile dipendente è data dai “Costi in Pubblicità” (il grafico di riferimento è costruito invertendo gli assi x e y); ne segue che, dopo aver inserito nella cella C6 il valore di 1.000.000, nella cella D6 utilizzeremo la funzione:
=TENDENZA(D2:D5;C2:C5;C6)
Pertanto, per ottenere un fatturato di un milione di euro dovremmo spendere in pubblicità 96.985,29 euro. Individuare correttamente le variabili dipendenti ed indipendenti prima della trascrizione della funzione TENDENZA è fondamentale in quanto un utilizzo improprio della stessa porta a dei risultati previsionali discordanti ma, soprattutto, privi di significato “matematico”. Ad esempio, se si sostituisce l’importo di 90.000 con 96.985,29 nel primo esempio proposto, non si ottiene un fatturato di un milione ma di 985.532,08 e ciò in quanto l’equazione della retta di interpolazione lineare è differente nei due esempi!
=> IT e Business: budget condivisi per innovare l’azienda
Esempio tre
Supponiamo di voler conoscere a quanto ammonteranno le vendite nei prossimi due esercizi utilizzando soltanto i “dati storici” relativi al fatturato. In questo caso si dovrà utilizzare come variabile indipendente gli anni e come variabile dipendente il fatturato; il valore y (fatturato) corrispondente al nuovo valore x (quinto anno) appartenente alla retta di interpolazione lineare, che calcoleremo nella cella C6 sarà, pertanto, pari a
=TENDENZA(C2:C5;B2:B5;B6)
mentre il fatturato previsionale relativo al sesto anno, che calcoleremo in C7, sarà pari a
=TENDENZA(C2:C5;B2:B5;B7)
Il fatturato previsto per il quinto anno sarà, pertanto, pari a 970.000 mentre quello relativo al sesto anno sarà pari a 1.030.000. Da notare che quest’ultimo valore poteva essere calcolato anche utilizzando nella funzione i valori relativi al primo anno di previsione, ovvero:
=TENDENZA(C2:C6;B2:B6;B7)

Il risultato sarebbe stato identico al precedente in quanto l’ultima coppia di valori x e y (5; 970.000) è già un punto della retta di interpolazione lineare e, pertanto, non influenza in alcun modo la previsione di tipo lineare.
La sintassi semplificata della funzione TENDENZA
Quando la variabile indipendente è formata da una serie numerica (ad esempio, 1, 2, 3, 4, …) si può omettere l’argomento x_nota (ma non il punto e virgola) e, quindi, utilizzare la “sintassi semplificata”:
=TENDENZA(y_nota;;nuova_x;cost)
Da notare che il valore dell’argomento nuova_x coincide, comunque, con il numero consecutivo della serie (e non comincia, quindi, da uno).
Tornando all’ultimo esempio proposto, la funzione
=TENDENZA(C2:C5;B2:B5;B6)
può essere scritta, più semplicemente, in questo modo:
=TENDENZA(C2:C5;;B6)









