


Esistono diversi metodi di calcolo che possono essere di aiuto nella scelta tra ipotesi alternative di investimento. In un articolo precedente ci siamo occupati del metodo del pay back period mentre, nel presente tutorial, ci occupiamo del metodo del Valore Attuale Netto (VAN) utilizzando alcuni esempi pratici elaborati nella cartella di lavoro in allegato.
=> Scarica l’esempio
La funzione VAN
Il Valore Attuale Netto (da ora in poi VAN) calcola il valore attuale (di oggi, per intenderci) di una serie di flussi di cassa generati in periodi futuri (che si presumono della stessa ampiezza, quali ad esempio, semestri o anni) attraverso l’utilizzo di un tasso di sconto (o meglio di un tasso di attualizzazione). Tra investimenti alternativi verrà considerato più conveniente quello che, oggi, vale maggiormente, ovvero ha un VAN maggiore. Il valore può essere calcolato numericamente grazie ad una semplice somma:
Funzione matematica del VAN
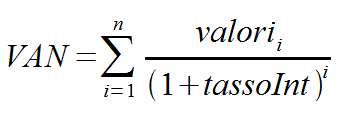
- i periodi ai quali si riferiscono i flussi (ad esempio, gli anni)
- valori flussi generati in ogni periodo (ad esempio, alla fine di ogni esercizio contabile)
- tassoInt tasso di attualizzazione relativo all’unità temporale utilizzata come periodo (nell’esempio, un anno)
Un esempio: scelta tra investimenti
Supponiamo di voler calcolare, utilizzando un tasso del 9%, il valore attuale netto di un investimento finanziario (ad esempio, l’acquisto di un impianto) che prevede un esborso iniziale di 20.000€ ed entrate (calcolate, ad esempio, sottraendo ai ricavi di vendita i costi annui di gestione) per 4.000€ alla fine del primo anno, per 7.000€ alla fine del secondo anno, 6.000€ alla fine del terzo anno e 5.000€ alla fine del quarto anno; supponiamo inoltre che alla fine del quarto anno l’impianto viene dimesso recuperando 2.000€ (valore di realizzo).
I flussi monetari relativi all’acquisto dell’impianto non devono essere attualizzati in quanto si riferiscono al periodo iniziale, o periodo 0 (20.000€ oggi, valgono 20.000€!), ma vanno comunque considerati come flussi negativi per determinare il valore complessivo dell’investimento; vanno, invece, attualizzati i flussi monetari dei tre periodi intermedi (4.000, 7.000 e 6.0000) e quelli relativi all’ultimo periodo costituiti dalle entrate effettive (5.000) e dalle entrate dovute alla dismissione dell’impianto (2.000). Pertanto, il VAN dell’investimento si calcolerà nel seguente modo:
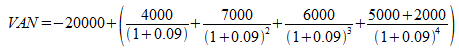
La funzione VAN di Excel
La funzione finanziaria VAN, appartenente alla categoria Finanziarie, ha la seguente sintassi:
=VAN(tasso_int;valore_1;valore_2;…;valore_n)
L’argomento tasso_int è il tasso di interesse relativo all’unità temporale considerata; pertanto, se i flussi sono di tipo semestrale ed il tasso di attualizzazione è annuale, occorrerà dividere quest’ultimo per due, se i flussi sono quadrimestrali il tasso annuale va diviso per 3, etc. Gli altri argomenti della funzione (valore_1, valore_2, …) rappresentano gli importi riscossi o pagati nelle diverse epoche; le entrate si indicano con il segno positivo mentre le uscite con segno negativo.
Considerato che un argomento è dato dal tasso di attualizzazione, su Excel consideriamo 29 importi nella funzione (è comunque possibile, se si utilizza una matrice come argomento, considerare qualsiasi numero di valori nella funzione ma, per semplicità di esposizione, evitiamo di trattare questo aspetto).
Nell’utilizzare la funzione finanziaria occorre fare attenzione al primo importo in quanto, poiché il calcolo del valore attuale netto si basa sui flussi di cassa futuri, esso non deve essere incluso come argomento della funzione VAN ma deve essere sommato algebricamente (come abbiamo osservato nell’esempio precedente) al risultato della funzione. Diversamente, se il primo importo viene sborsato alla fine del primo periodo (ad esempio, si ha una dilazione di un anno per il suo pagamento), rientra normalmente come argomento della funzione VAN.
Il foglio elettronico di esempio
Trascriviamo i dati dell’esempio precedente su di un foglio di calcolo come rappresentato in figura e utilizziamo la funzione VAN per determinare la convenienza dell’investimento (acquisto di un nuovo impianto).

La funzione VAN (costruita con riferimenti numerici) da utilizzare per il calcolo del valore attuale netto è
=VAN(9%;4000;7000;6000;5000+2000)+(-20000)
Come si può osservare nella funzione VAN non è stato inserito l’esborso iniziale (riferito al periodo 0) mentre nel quarto periodo sono stati sommati gli introiti relativi al periodo e quelli relativi alla vendita dell’impianto; il valore dell’esborso iniziale, indicato con segno negativo (-20000) è stato sommato algebricamente al risultato della funzione VAN.
Se si utilizzano, pertanto, i riferimenti alle celle del prospetto, in C8 dobbiamo trascrivere la seguente funzione:
=VAN(C7;C3;C4;C5;C6)+C2
Il risultato della formula è negativo (pari a -846,44€) e, pertanto l’acquisto e l’utilizzo dell’impianto non è conveniente. Da notare che un semplice calcolo algebrico tra i valori avrebbe portato a ritenere la fattibilità dell’investimento in quanto i flussi positivi sono pari a 24.000€ (4000+7000+6000+7000) mentre quelli negativi sono pari a 20000 (l’esborso iniziale per l’acquisto dell’impianto). La differenza tra i due risultati è dovuta al tasso di attualizzazione che “sconta” il valore futuro per determinare l’equivalente ad oggi (riscuotere 7000€ tra quattro anni non è come riscuoterli oggi).
Un altro esempio: scelta di acquisto
Supponiamo di dover acquistare dei distributori automatici da mettere in diversi punti vendita per un periodo di due anni; i due modelli (distributore X e Y) hanno un costo differente e generano dei flussi semestrali (dati dai ricavi di vendita meno i costi dei prodotti venduti sommati a quelli di gestione dei distributori) come rappresentato nel foglio elettronico sottostante.
Ipotizzando un tasso di attualizzazione annuale del 10%, su quale tipo di distributore orientiamo la nostra scelta?
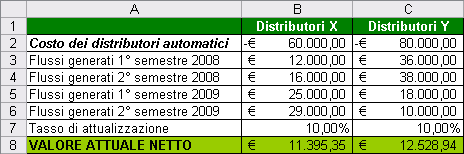
Nell’esempio proposto, abbiamo utilizzato dei flussi di cassa che, algebricamente sommati con il costo dei distributori, generano un pari introito alla fine dei due anni (22.000€); pertanto, da un punto di vista strettamente matematico (ovvero senza considerare gli aspetti finanziari) risulterebbe indifferente la scelta di uno dei due modelli. Analizziamo ora gli aspetti finanziari attraverso l’utilizzo della funzione VAN.
Per determinare il valore attuale netto del primo investimento nella cella B8 dobbiamo inserire la seguente formula:
=VAN(B7/2;B3;B4;B5;B6)+B2
Poiché il tasso di attualizzazione è espresso in anni mentre i flussi generati dai due possibili investimenti sono semestrali, è necessario dividere il tasso percentuale per 2. Pertanto il primo argomento della funzione sarà B7/2; gli altri argomenti della funzione rappresentano i flussi di cassa generati nei quattro periodi dai Distributori X. Per determinare, infine, il valore attuale netto dell’investimento (pari a 11.395€), è necessario sommare algebricamente al risultato della funzione VAN il valore del costo dei distributori automatici (posto nella cella B2 con segno negativo). Una formula simile è stata utilizzata per determinare il valore attuale netto dei Distributori Y (pari a 12.529€); nella cella C8, difatti, è stata inserita la formula:
=VAN(C7/2;C3;C4;C5;C6)+C2









