


Immaginiamo che ci venga chiesto di pianificare un Project Portfolio, costituito dalle due commesse seguenti:
| Activity Name |
Original Duration [d] |
Predecessor(s), Relationship Type(s) & Lag(s) [d] |
Successor(s), Relationship Type(s) & Lag(s) [d] |
Resource(s) |
Budgeted Labor Units [h] |
| A100 | 2 d | None |
A110, FS, 0 d |
R1 | 16 h |
| A110 | 5 d | A100, FS, 0 d | A130, FS, 0 d | R1 | 40 h |
| A120 | 2 d | A100, FS, 1 d | A130, FS, 0 d | R5 | 16 h |
| A130 | 3 d | A110, FS, 0 d A120, FS, 0 d |
None | R1 | 24 h |
Tabella 21. Il modello reticolare del progetto A.
|
Activity Name |
Original Duration [d] |
Predecessor(s), Relationship Type(s) & Lag(s) [d] |
Successor(s), Relationship Type(s) & Lag(s) [d] |
Resource(s) |
Budgeted Labor Units [h] |
|
B100 |
2 d |
None |
B110, FS, 0 d B120, FS, 1 d |
R2 |
16 h |
|
B110 |
5 d |
B100, FS, 0 d |
B130, FS, 0 d |
R3 |
40 h |
|
B120 |
2 d |
B100, FS, 1 d |
B130, FS, 0 d |
R5 |
16 h |
|
B130 |
3 d |
B110, FS, 0 d B120, FS, 0 d |
None |
R4 |
24 h |
Tabella 22. Il modello reticolare della commessa B.
Immaginiamo che entrambi i progetti inizino lunedì 6 novembre 2017 e che non ci sia alcuna data di fine contrattuale.
Applicando il Critical Path Method alla commessa A, si ottiene la soluzione seguente:
|
Activity Name |
Original Duration [d] |
Start |
Finish |
Total Float [d] |
|
A100 |
2 d |
06/11/17 |
07/11/17 |
0 d |
|
A110 |
5 d |
08/11/17 |
14/11/17 |
0 d |
|
A120 |
2 d |
09/11/17 |
10/11/17 |
2 d |
|
A130 |
3 d |
15/11/17 |
17/11/17 |
0 d |
Tabella 23. Le date d’inizio e fine dei Task del progetto A.
Applicando il Critical Path Method alla commessa B, si ottiene la soluzione seguente:
|
Activity Name |
Original Duration [d] |
Start |
Finish |
Total Float [d] |
|
B100 |
2 d |
06/11/17 |
07/11/17 |
0 d |
|
B110 |
5 d |
08/11/17 |
14/11/17 |
0 d |
|
B120 |
2 d |
09/11/17 |
10/11/17 |
2 d |
|
B130 |
3 d |
15/11/17 |
17/11/17 |
0 d |
Tabella 24. Le date d’inizio e fine dei Task del progetto B.
Le soluzioni presentate nelle Tabelle 23 e 24 sono illustrate nella Figura seguente:
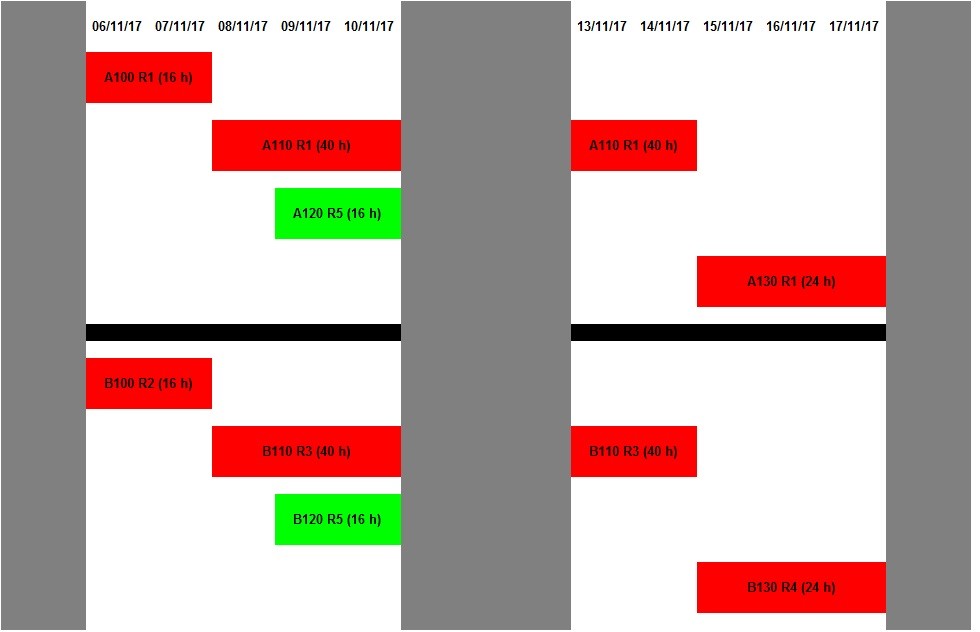
Il carico di lavoro delle cinque risorse R1, R2, R3, R4 e R5 è il seguente:
| Risorsa | 06/11 | 07/11 | 08/11 | 09/11 | 10/11 | 13/11 | 14/11 | 15/11 | 16/11 | 17/11 |
| R1 | 8 h | 8 h | 8 h | 8 h | 8 h | 8 h | 8 h | 8 h | 8 h | 8 h |
| R2 | 8 h | 8 h | 0 h | 0 h | 0 h | 0 h | 0 h | 0 h | 0 h | 0 h |
| R3 | 0 h | 0 h | 8 h | 8 h | 8 h | 8 h | 8 h | 0 h | 0 h | 0 h |
| R4 | 0 h | 0 h | 0 h | 0 h | 0 h | 0 h | 0 h | 8 h | 8 h | 8 h |
| R5 | 0 h | 0 h | 0 h | 16 h | 16 h | 0 h | 0 h | 0 h | 0 h | 0 h |
Tabella 25. Si noti il sovraccarico della risorsa R5, giovedì 9 e venerdì 10 novembre 2017.
Come si può notare, alla risorsa R5 viene chiesto:
- di svolgere il Task A120 nei giorni giovedì 9 e venerdì 10 novembre 2017 (percentuale d’impiego = 100%);
- di eseguire l’attività B120 nei giorni giovedì 9 e venerdì 10 novembre 2017 (percentuale d’impiego = 100%).
Se la risorsa R5 è disponibile 8 ore/giorno lavorativo, è evidente che:
- la soluzione di cui alla precedente Tabella 23 è ammissibile per la commessa A, purché considerata singolarmente (vale a dire senza tener conto del fatto che, in realtà, c’è anche il progetto B);
- la soluzione di cui alla precedente Tabella 24 è ammissibile per la commessa B, purché considerata singolarmente (vale a dire senza tener conto del fatto che, in realtà, c’è anche il progetto A);
- la soluzione di cui alla Figura 15 non è ammissibile per l’intero portafoglio (= commessa A + progetto B).
Che strategia adottare?
Si potrebbe notare che il Task A120 e l’attività B120 hanno:
- la medesima durata, pari a 2 d;
- lo stesso scorrimento totale, pari a 2 d.
Quindi, si potrebbe raddoppiare la durata sia del Task A120 sia dell’attività B120, che passerebbe da 2 d a 4 d, dimezzando la percentuale d’impiego della risorsa R5, che passerebbe da 100% a 50%. La Tabella seguente illustra il nuovo carico di lavoro delle cinque risorse R1, R2, R3, R4 e R5:
| Risorsa | 06/11 | 07/11 | 08/11 | 09/11 | 10/11 | 13/11 | 14/11 | 15/11 | 16/11 | 17/11 |
| R1 | 8 h | 8 h | 8 h | 8 h | 8 h | 8 h | 8 h | 8 h | 8 h | 8 h |
| R2 | 8 h | 8 h | 0 h | 0 h | 0 h | 0 h | 0 h | 0 h | 0 h | 0 h |
| R3 | 0 h | 0 h | 8 h | 8 h | 8 h | 8 h | 8 h | 0 h | 0 h | 0 h |
| R4 | 0 h | 0 h | 0 h | 0 h | 0 h | 0 h | 0 h | 8 h | 8 h | 8 h |
| R5 | 0 h | 0 h | 0 h | 8 h | 8 h | 8 h | 8 h | 0 h | 0 h | 0 h |
Tabella 26. Adesso, la risorsa R5 non è più sovraccarica.
La Figura seguente illustra il nuovo programma lavori:
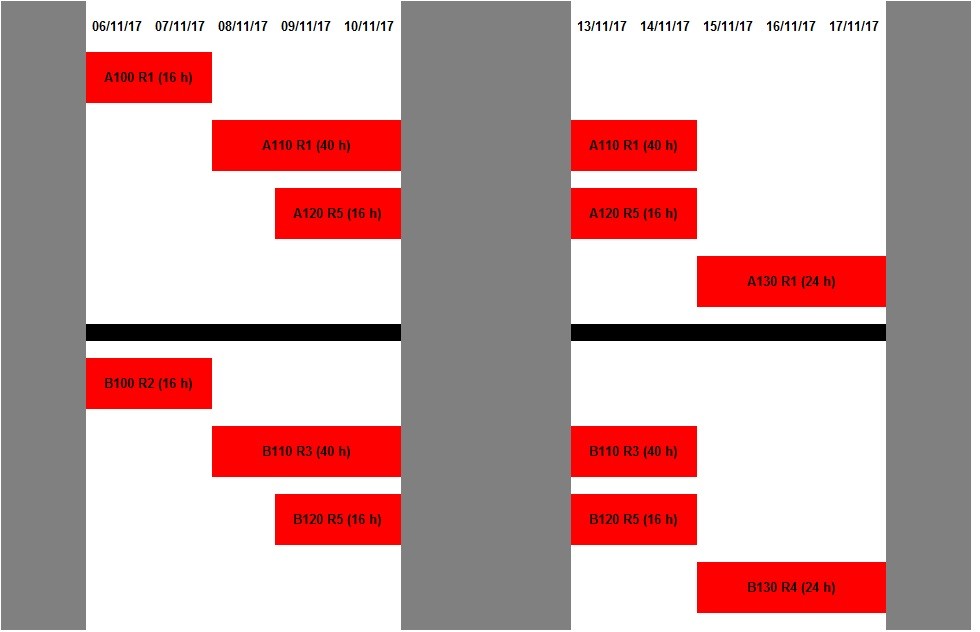
|
Activity Name |
Original Duration [d] |
Start |
Finish |
Total Float [d] |
|
A100 |
2 d |
06/11/17 |
07/11/17 |
0 d |
|
A110 |
5 d |
08/11/17 |
14/11/17 |
0 d |
|
A120 |
4 d |
09/11/17 |
14/11/17 |
0 d |
|
A130 |
3 d |
15/11/17 |
17/11/17 |
0 d |
Tabella 27. Le nuove date d’inizio e fine dei Task della commessa A.
|
Activity Name |
Original Duration [d] |
Start |
Finish |
Total Float [d] |
|
B100 |
2 d |
06/11/17 |
07/11/17 |
0 d |
|
B110 |
5 d |
08/11/17 |
14/11/17 |
0 d |
|
B120 |
4 d |
09/11/17 |
14/11/17 |
0 d |
|
B130 |
3 d |
15/11/17 |
17/11/17 |
0 d |
Tabella 28. Le nuove date d’inizio e fine dei Task del progetto B.
Esistono anche delle altre soluzioni ammissibili per l’intero portafoglio, del tutto equivalenti a quella appena illustrata, poiché producono il medesimo risultato (stesse date d’inizio e fine e identici scorrimenti totali). Esse sono descritte dalla relazione seguente:
Budgeted Labor Units(R5, A120, t) + Budgeted Labor Units(R5, B120, t) = 8 ore/giorno lavorativo [1]
(con t = 09/11, 10/11, 13/11 o 14/11)
Il primo addendo, Budgeted Labor Units(R5, A120, t), indica quante ore/uomo della risorsa R5 sono state assegnate (nella fase di pianificazione) all’attività A120, il giorno lavorativo t (09/11, 10/11, 13/11 o 14/11).
Il secondo addendo, Budgeted Labor Units(R5, B120, t), indica quante ore/uomo della risorsa R5 sono state assegnate (nella fase di pianificazione) al Task B120, il giorno lavorativo t (09/11, 10/11, 13/11 o 14/11).
Al variare di t (09/11, 10/11, 13/11 o 14/11), Budgeted Labor Units(R5, A120, t) esprime la legge h1 = f(t) con cui le ore/uomo della risorsa R5 si distribuiscono sulla durata dell’attività A120.
Al variare di t (09/11, 10/11, 13/11 o 14/11), Budgeted Labor Units(R5, B120, t) esprime la legge h2 = g(t) con cui le ore/uomo della risorsa R5 si distribuiscono sulla durata del Task B120.
Poiché il carico di lavoro della risorsa R5 è dato dalla somma di h1 e h2, affinché la risorsa R5 non sia sovraccarica, deve essere soddisfatta la relazione seguente:
h1 + h2 = f(t) + g(t) ≤ 8 ore/giorno lavorativo [2]
(con t = 09/11, 10/11, 13/11 o 14/11)
Si noti che, nelle precedenti relazioni [1] e [2], il termine noto, a secondo membro, esprime la disponibilità giornaliera della risorsa, supposta pari a 8 ore/giorno lavorativo.
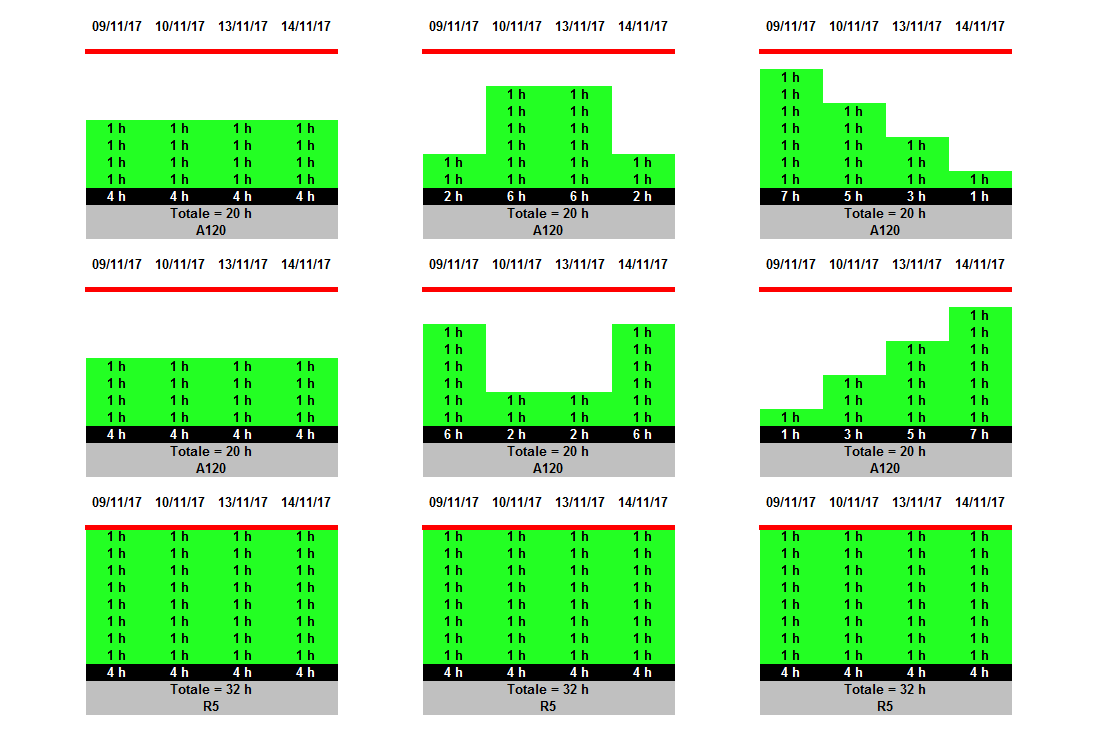
Si ottiene la soluzione ammissibile per l’intero portafoglio illustrata nella precedente Tabella 26, quando, per ogni valore assunto da t (09/11, 10/11, 13/11 o 14/11), è soddisfatta la relazione seguente:
Budgeted Labor Units(R5, A120, t) = Budgeted Labor Units(R5, B120, t) = 4 ore/giorno lavorativo
Come discusso nel precedente articolo (Pianificazione multiprogetto: spezzare le attività), il fatto che la risorsa R5 debba dividersi fra l’attività A120 e il Task B120, passando dall’esecuzione della prima allo svolgimento del secondo (e/o viceversa) una o più volte/giorno lavorativo, è contrario ai principi dell’approccio noto come Critical Chain Project Management. Se, per esempio, le attività in questione avessero luogo in due differenti reparti produttivi, bisognerebbe prendere in considerazione anche il trasferimento da un reparto all’altro, che comporterebbe un’inevitabile perdita di tempo, dando vita, quindi, a un’inefficienza.
Ricordo che, Coeteris Paribus, un processo è più efficiente di un altro, se consuma meno Input per produrre la medesima quantità di Output, oppure se a parità d’Input consente di ottenere più Output.
______________
L’autore dedica questo articolo alla memoria di Francesco Turra, Studente di Logistica che conosce già i mille segreti del nostro affascinante Universo.









