


Utilizzando un semplice foglio di calcolo Excel, sono diverse le funzioni finanziarie che consentono di attualizzare il valore degli introiti e degli esborsi monetari scaturiti da specifici investimenti, così da valutare la convenienza tra ipotesi alternative.
Finanziamenti: convenienza a confronto
Le stesse funzioni possono essere utilizzate, con qualche “correzione”, per determinare la convenienza finanziaria di finanziamenti alternativi: a differenze degli investimenti, il capitale iniziale di un prestito rappresenta infatti un’entrata dal punto di vista finanziario, mentre i flussi monetari periodici rappresentano un esborso finanziario. In questo tutorial proponiamo un modello finanziario che consente di comparare la convenienza tra un contratto di mutuo ed uno di leasing.
=> Scarica l’esempio di calcolo
Il modello di calcolo da scaricare
Con le funzioni VAN e VA di Excel, e con le rispettive funzioni “inverse” TIR e TASSO, attraverso un calcolo interattivo è possibile determinare il tasso di rendimento dei flussi monetari e, di conseguenza, di operare una scelta tra investimenti alternativi senza una preventiva stima del tasso di attualizzazione. La funzione più “adatta” in questo caso è quella VA (e, congiuntamente o in alternativa, la funzione TASSO) per almeno due ragioni:
- la rata di mutuo e il canone di locazione sono costanti nel tempo e, pertanto, in una simile ipotesi la funzione VA è da preferire alla funzione VAN;
- i flussi monetari generati dalle due ipotesi di finanziamento possono essere sia anticipati che posticipati (generalmente i canoni di locazione sono pagati anticipatamente, mentre le rate dei mutui alla fine di ogni periodo) e, pertanto, è impossibile utilizzare la funzione VAN in simili ipotesi.
Confronto tra finanziamenti: un esempio pratico
Per comprendere come utilizzare il modello in una ipotesi di finanziamento, utilizziamo un esempio pratico. Supponiamo di voler acquistare un bene strumentale del valore di 280.000 € e di trovarci di fronte alle due seguenti ipotesi di finanziamento:
- stipulare un contratto di mutuo che preveda l’esborso di una rata semestrale posticipata del valore di 32.000 € per un periodo di sei anni
- stipulare un contratto di leasing che preveda il pagamento di un canone quadrimestrale anticipato del valore di 21.000 €, sempre per un periodo di sei anni, e che offra la possibilità di riscattare il bene al termine del contratto pagando una cifra di 6.000 €
Supponendo un tasso di attualizzazione del 5% e la possibilità di vendere il bene al termine del sesto anno ad un prezzo di 12.000 €, quale tra le due ipotesi di finanziamento risulta più conveniente? Trasferiamo i dati riportati nell’esempio all’interno di un foglio di calcolo così come rappresentato in figura.
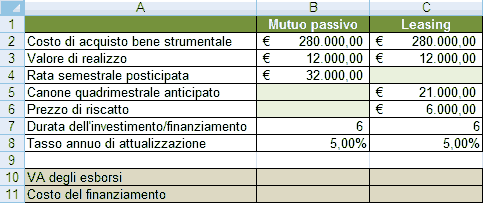
Iniziamo col notare che le due ipotesi di finanziamento sembrano “equivalenti” in quanto l’esborso da sostenere in caso di mutuo (dato da 32.000 € * 2 semestri * 6 anni) è uguale a quello previsto dal contratto di leasing (21.000 € * 3 quadrimestri * 6 anni + 6.000 € per il riscatto) ovvero pari a 384.000 €. In realtà, come vedremo a breve, da un punto di vista finanziario esiste una convenienza verso una delle due scelte di finanziamento. Calcoliamo innanzitutto il Valore Attuale degli esborsi monetari nell’ipotesi di mutuo (cella B10). Ricordiamo, prima di proseguire, la sintassi della funzione VA: =VA(tasso_int;periodi;pagamento;valore_futuro;tipo)
L’argomento tasso_int è dato dal tasso di attualizzazione presente nelle celle B8 rapportato ai periodi presenti in un anno: essendo la rata del mutuo semestrale il suo valore è pari a 2,50% (ovvero B8/2). L’argomento periodi è dato dal totale delle rate da pagare nei sei anni, ovvero dalla moltiplicazione tra la cella B7 (durata in anni del finanziamento) e 2 (in un anno vengono pagate due rate semestrali). L’argomento pagamento è dato dal valore (costante) delle singole rate posto nella cella B4: trattandosi di un esborso monetario è necessario assegnare al riferimento di cella il segno meno (-). L’argomento valore_futuro è dato dal valore di realizzo al termine dei sei anni (cella B3): trattandosi di una entrata il valore va indicato con il segno positivo. Infine, l’argomento tipo può essere omesso in quanto si tratta di pagamenti posticipati. Riepilogando, nella cella B10 scriveremo, pertanto, la formula: =VA(B8/2;B7*2;-B4;B3)
Il risultato che si ottiene dalla formula (319.325,80 €) indica il valore attuale dei flussi di cassa negativi (le rate pagate alle singole scadenze) sommato algebricamente al flusso di cassa positivo dovuto alla vendita del bene al termine del sesto anno. Da notare che il valore ottenuto è di gran lunga inferiore al valore algebrico calcolato in precedenza (384.000 €) in quanto i pagamenti diluiti nel tempo vengono attualizzati ad oggi “scontandoli” ad un tasso di attualizzazione del 5%.
- Il costo effettivo del finanziamento con contratto di mutuo è dato dalla differenza tra il valore attuale degli esborsi e il valore del bene acquistato pertanto nella cella B11 si utilizza la formula: =B23-B2, che dà come risultato 39.325,80 € (319.325,80 € – 280.000,00 €).
Per calcolare il VA degli esborsi nel caso di leasing è stata utilizzata nella cella C10 la funzione: =VA(C8/3;C7*3;-C5;C3-C6;1). L’argomento tasso_int della funzione è stato diviso per 3 mentre l’argomento periodi è stato moltiplicato per 3 che rappresenta i pagamenti effettuati in un anno (canoni quadrimestrali); l’argomento pagamento, corrisponde, come nella funzione precedente relativa al mutuo, all’esborso monetario necessario per pagare periodicamente il canone (-C5); il quarto argomento della funzione, valore_futuro, è dato dalla differenza tra il flusso monetario positivo (cella C3 12.000 €) dovuto alla vendita del bene e quello negativo (6.000 €) dovuto all’esborso monetario necessario per riscattare il bene; infine, poiché i canoni di locazione sono pagati all’inizio di ogni periodo, è stato utilizzato 1 come argomento ipotesi.
- Il costo effettivo del finanziamento con contratto di leasing (cella C11) pari a 45.206,61 € è dato, come per il mutuo, dalla differenza tra il valore attuale degli esborsi ottenuti dalla formula precedente (325.206,61 €) e il valore del bene strumentale (cella B2).
Il metodo del Valore Attuale dimostra, pertanto, che nell’acquisizione del bene strumentale è preferibile stipulare il contratto di mutuo in quanto consente, a differenza del contratto di leasing, di risparmiare circa 6.000 € (45.206,61 € – 39.325,80 €).
Come scegliere tra i due finanziamenti
Abbiamo in precedenza affermato che la funzione TASSO consente di scegliere tra investimenti/finanziamenti alternativi senza dover ricorrere alla stima del tasso di attualizzazione. La funzione restituisce un valore che, sostituito al tasso di attualizzazione della funzione VA, consente di ottenere flussi monetari in entrata pari a quelli in uscita ovvero, detto in altri termini, consente di azzerare il Valore Attuale. A differenza delle ipotesi di investimento, nella scelta tra finanziamenti alternativi è da preferire quello che presenta un valore percentuale più basso.
Riprendiamo, per semplicità espositiva (ma anche per verificare la correttezza delle formule che utilizzeremo), i dati dell’esempio precedente; duplichiamo il foglio di lavoro e sostituiamo il contenuto delle righe 10 e 11 come riportato in figura. Ricordiamo innanzitutto la sintassi della funzione TASSO, costituita da sei argomenti: =TASSO(periodi;pagamento;val_attuale;val_futuro;tipo;ipotesi). La funzione da inserire nella cella B10 è: =TASSO(B7*2;-B4;+B2;B3)
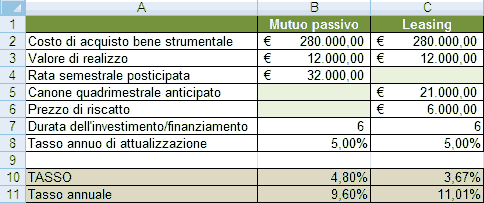
L’argomento periodi è dato dal numero totale delle rate del mutuo (B7*2); l’argomento pagamento è dato dal valore (cella B4) della rata semestrale (trattandosi di flussi monetari in uscita si indicano con segno algebrico negativo); l’argomento val_attuale è dato dal costo (cella B2) del bene strumentale (esso va indicato con segno positivo in quanto rappresenta un introito dal punto di vista finanziario, rappresentato appunto dalla somma ricevuta attraverso il contratto di mutuo!); l’argomento valore_futuro è dato dai flussi monetari (anch’essi positivi) che si ottengono a seguito della vendita del bene (B3); l’argomento tipo può essere omesso in quanto siamo in presenza di flussi posticipati, mentre l’argomento ipotesi può essere omesso per lasciare ad Excel il compito di determinare il risultato per interazione.
Nella cella B11 è stato calcolato il tasso annuale (9,60%) moltiplicando per due il tasso semestrale ottenuto nella cella B10.
Nella cella C10 è stata utilizzata la seguente funzione: =TASSO(C7*3;-C5;+C2;C3-C6;1)
A differenza della funzione precedente, l’argomento periodi si riferisce al numero degli anni (C7) moltiplicato per 3 annualità (il canone è quadrimestrale), l’argomento val_futuro è dato dalla differenza tra il valore di realizzo (C3) e il costo da sostenere per riscattare il bene (C6); infine, per l’argomento tipo è stato utilizzato 1 in quanto il pagamento dei canoni è anticipato. Nella cella C11 è stato calcolato il tasso annuale (11,01%) moltiplicando per tre il tasso quadrimestrale ottenuto nella cella C10. Confrontando i due tassi annuali si può sostenere che il finanziamento da preferire per l’acquisto del bene strumentale è il contratto di mutuo in quanto presenta un TASSO minore rispetto al contratto di leasing. Tale affermazione può essere dimostrata sostituendo il valore TASSO di uno dei due finanziamenti al Valore Attuale calcolato nell’esempio precedente.
Ad esempio, se si utilizza un tasso di attualizzazione annuale del 9,60%, il Valore Attuale degli esborsi relativi al contratto di mutuo è pari a 280.000 € (ovvero pari al costo del bene) mentre il Valore Attuale degli esborsi relativi al contratto di leasing è pari a 289.671,87 €. Pertanto, se il tasso di attualizzazione reale è del 9,60% il contratto di mutuo è da preferire in quanto si risparmiano 289.671,87 € Diversamente, se si utilizza un tasso di attualizzazione annuale dell’11,01% il VA degli esborsi relativi al contratto di leasing è pari a 280.000 € mentre quello relativo al contratto di mutuo è pari a 269.399,51 €. Pertanto, se il tasso di attualizzazione reale è dell’11,01% il contratto di mutuo è da preferire in quanto si “risparmiano” circa 11.000 € (il VA del bene acquisto è di 280.000 €!).
In entrambi i casi è quindi preferibile il contratto di mutuo. È importante notare che la differenza tra i due finanziamenti varia al variare del tasso di attualizzazione ma la convenienza del mutuo è sempre mantenuta.









